Bubble Plumes
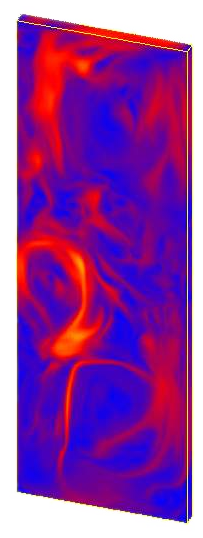
Bubbly flows are encountered in many fields of engineering, associated with different spatial scales. At small scale, they are found for instance in metallurgy in gas stirring of molten metals in ladles, in nuclear devices, and in chemical reactors. At extremely large scale, they take place in induced events of CO2 sequestration, by which this compound is intentionally pumped into deep seas to distract it from the atmosphere. At the environmental scale, the application range is vast: bubble plumes have been used as barriers to contain density intrusions or oil spills, as breakwaters, as silt curtains, and for destratification purposes in lakes. In sanitary engineering, bubble plumes are usually employed for aeration purposes in water and wastewater treatment plants. Additionally, arrays of bubble diffusers are used in reservoirs aimed at storing Combined Sewer Overflows (CSO), in order to avoid the occurrence of anaerobic conditions. The presence of bubbles in most of the early applications of bubble plumes was only instrumental in producing a current, while mass transfer effects and internal details of the plumes were not of special interest. In aeration bubble plumes, however, mass transfer effects and phenomena associated with air-water interfaces are extremely important. Therefore a detailed description of the effects of breakup and coalescence of bubbles and of plume wandering becomes of primary concern in the study of aeration bubble plumes. Since the characteristics of such phenomena strongly depend on the level of turbulence within the container, a clear need for a detailed description of turbulence in bubble plumes emerges. This presentation is devoted to the analysis of different strategies for the modeling of turbulence in dilute bubble plumes, based on the multi- component fluid theory. The application motivating this endeavor is the development of numerical models for the design of reservoirs containing CSO. An approach based on a two-fluid model is presented and discussed, with the goal of obtaining satisfactory answers to several “two-phase turbulence” issues: 1) how to represent the bubble dispersion by the turbulence; 2) how to model the mass transfer effects in bubble plumes; 3) how to capture plume wandering; 4) how to include breakup and coalescence; and 5) how to model the turbulence “modulation” by the disperse phase. Defining a two-level averaging and under the umbrella of dilute bubble plumes, a set of equations is established, which can be organized as a hierarchy of models. The hierarchy of models is intended to deal with different field conditions and scales. Turbulence is modeled with a – model and a Large-Eddy Simulation (LES) approach, in a consistent way. All of the above turbulence issues have been considered. As a verification of the consistency of the models, it is shown that when these equations are integrated in horizontal planes, they yield the well-known integral models of bubble plumes. A comparison of gross parameters coming from a two- dimensional, axisymmetric solution, with one coming from a 1-D model, gives close agreement. This allows for the computation of the entrainment coefficient and of the void-to-momentum spread ratio from the 2-D solution, obtaining a satisfactory agreement with laboratory experiments. After the demonstration of successful comparisons with other laboratory datasets coming from the metallurgical field, attention turns to the study of plume wandering phenomena in a box. Results of two dynamic simulations using both turbulence treatments, but with a relatively “simple” model, show that wandering can be reproduced numerically without the unnecessary complexity found in some papers. The run based on LES is also used to characterize the coherent structures that appear in the interplay of the bubble plume and the walls of the box, and with regions of different vorticity. Finally, a submodel for breakup and coalescence based on the Boltzmann equation is introduced, showing that these effects can produce important changes close to the diffuser in small-scale vessels. The presentation closes with a general understanding regarding how efficient some very complex modeling approaches really are, and with a message that modeling turbulence in bubble plumes, as with any other phenomenon, can only be successful when the main physical mechanisms are included in the models.
Media
Animation of model [MPEG, 14 MB]